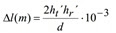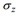Modelo de Propagación de tierra Plana
El caso más simple para iniciar el estudio de la propagación en la cercanía de la superficie terrestre es el de suponer a las antenas transmisora y receptora a una distancia tal, que puede ignorarse la curvatura de la tierra y suponerla como una superficie plana e imperfectamente conductora. Adicionalmente se supone que la superficie es lisa y uniforme a lo largo del trayecto de propagación. Estas suposiciones son válidas en numerosas situaciones prácticas. Los cálculos de propagación en la cercanía de la superficie terrestre requieren del conocimiento de las características eléctricas de dicha superficie y, aunque no es posible conocerlas con precisión detallada, en la tabla siguiente se dan algunos valores típicos adecuados para dichos cálculos.
En la tabla, εr es la permitividad relativa o constante dieléctrica y σ la conductividad en Siemens/m.
El caso más simple de propagación sobre tierra
plana se ilustra en la figura
En este caso, la energía
electromagnética llega al receptor por dos trayectorias diferentes, una
directa, r1
y otra,
resultado de la reflexión especular en la superficie terrestre, r2. Como la trayectoria reflejada
es más larga que la directa, habrá una diferencia de fase entre las dos
componentes del campo eléctrico que llegan al receptor.
La
intensidad de campo que llega al receptor por la trayectoria directa se puede obtener
a partir de , en que la potencia isotrópica equivalente
radiada se substituye por:
Donde PAT es la potencia de entrada a la antena transmisora y G1 es su ganancia directiva en la
dirección del rayo directo, r1, con lo que:
En la expresión anterior se ha omitido el término
que expresa la variación en el tiempo, ejωt. Análogamente, la intensidad de
campo en el receptor, debida al rayo reflejado se puede obtener calculando
primero la diferencia en longitud de las dos trayectorias: la directa y la
reflejada:
Si G2 es la ganancia de la antena transmisora en la
dirección de salida del rayo reflejado, r2 y ρ es
el coeficiente de reflexión en el punto A, en general, complejo:
En la mayoría de los casos
prácticos, la altura de las antenas transmisora y receptora es mucho menor que
la distancia entre ellas y es válido asumir que r1 ≈ r2 y, además, el ángulo de reflexión
φ es muy pequeño, con lo que
también es válido suponer que la ganancia directiva de la antena transmisora es
la misma en la dirección del rayo directo que en la dirección del rayo
reflejado.
La intensidad total de campo
eléctrico en el receptor es la suma de las dos componentes: la debida al rayo
directo y la debida al rayo reflejado:
Donde
Siendo
Y el factor de atenuación del campo
Donde
El ángulo de reflexión, φ,
puede expresarse en términos de la altura de las antenas y de la distancia
entre ellas como:
Y la diferencia de distancia Δr
como:
De acuerdo a lo anterior, el factor de atenuación
del campo, αE puede expresarse ahora en función
de la altura de las antenas transmisora y receptora:
Según varía r1 el valor de αE alcanza valores máximos o mínimos
cuando:
Así, en los máximos, αE = 1 + |ρ|
y en los mínimos, αE = 1 - |ρ|.
En los máximos, las componentes directa y reflejada del campo se combinan
aditivamente y el campo total es mayor que el debido sólo a la trayectoria
directa, en tanto que en los mínimos la combinación es substractiva. Esta forma
de variación de αE se ilustra en la figura de a continuación
Una consecuencia importante es
que, a una distancia fija entre las antenas transmisora y receptora, las
variaciones en la altura de la antena receptora dan lugar a un patrón de
atenuación semejante al de la figura de abajo con la gráfica girada 90º.
Esto es de interés en la práctica al instalar la antena receptora, ya que debe
buscarse la altura óptima de ésta para conseguir el nivel máximo de señal.
Figura de variación del factor de atenuación
De lo anterior se infiere que,
dependiendo del coeficiente de reflexión y de la diferencia de longitud entre
las trayectorias directa y reflejada, la intensidad de campo en el punto de
recepción y, por consecuencia el voltaje inducido en la antena receptora puede
ser mayor o menor que el que se tendría en condiciones de espacio libre en que
sólo se tiene la trayectoria directa. El caso tratado en esta sección es
bidimensional y sólo considera una reflexión y es el caso más simple de lo que
se designa como propagación multicamino. En situaciones reales, los
entornos de propagación son siempre tridimensionales y por lo general, se
tienen numerosas trayectorias que contribuyen a veces al aumento de la potencia
recibida, si bien en los casos más habituales, dan lugar a atenuación
considerable en el medio de propagación.
El análisis realizado en esta
sección corresponde al modelo de tierra plana y su aplicación es válida
a distancias hasta de unos 10 km entre las antenas, en que la curvatura de la
tierra no es significativa.
¿QUE DATOS BRINDA LA RECOMENDACIÓN UIT-R P.527-3?
¿Y EN QUE AYUDA?
