Modelo Propagación de Tierra
Curva
Modelo de tierra curva
Modelo
que se aplica cuando la longitud del enlace es del orden de la distancia de visibilidad
radioeléctrica o mayor.
Si las protuberancias debidas a la curvatura
terrestre son superiores a unos 5 m, el modelo de Tierra plana deja de ser
válido, pasando a regir el modelo de Tierra curva. Esto sucede para longitudes
del orden de la distancia de visibilidad radioeléctrica o mayores. En este
modelo se considera una trayectoria del rayo rectilínea y una Tierra ficticia
de radio R’0=kR0. Se supone una Tierra lisa, como sucede en propagación sobre
mar, grandes lagos o llanuras con terreno muy poco ondulado.
Perfiles y
condiciones
Se toma la siguiente notación
•x: distancia del transmisor a un punto, (km)
•c(x): altura del terreno so bre el nivel del mar,
(m)
•f(x):protuberanciade la tierra o flecha (m)
•h(x): despejamiento
o altura del rayo directo sobre el terreno, en metros
Tierra curva: si la flecha (f(x) máx) es mayor de 5
metros.
¿Cuando deja de ser válido el modelo de tierra
plana?:
Distancias del orden de la distancia de visibilidad
radioeléctrica
Alcance, distancia de visibilidad radioeléctrica:
suma de las distancias de horizonte
Objetivo: Calcular las pérdidas para : Trayectoria rectilinea, y kR0.
Se trata de asimilar el modelo de tierra curva al
modelo de tierra plana
Para ello
1. Se calculan unas ht’ y hr’ Y calculamos el
desfase ∆
2. Se comprueba que la tierra no obstaculice el
enlace
3. Se actualiza el coeficiente de reflexión R
Con la
divergencia
Con la
rugosidad del terreno
4. Se calculan las pérdidas
Modelo de Reflexión, sobre tierra curva
Una vez calculadas d1 y d2 (en km), se calculan las alturas
Y el ángulo de incidencia en miliradianes
El límite sobre el cual se puede aplicar óptica geométrica,
La diferencia de recorridos
La diferencia de fases,
La reflexión sobre superficie esférica convexa
produce divergencia que se traduce en reducción aparente del coeficiente de
reflexión,
Se puede además corregir el coeficiente de Reflexión
introduciendo una atenuación (en el RR) debida a la rugosidad del terreno
•Donde Δ se calcula con ht’ y hr’
•Y Re se ha actualizado convenientemente
Y la
pérdida básica de propagación












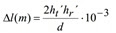




No hay comentarios.:
Publicar un comentario